The Cut That Says “Please”
Faulty Instructions, Desire, Lacan’s Metaphor, Borromean Topology, and the Golden Ratio’s Shadow
Iraj E. Ghoochani
Please Me (and Read This) — If It Pleases You
The following reflections arose from an exchange with my long-time co-conspirator in thought, Don. Kunze. Our correspondence often unfolds like a séance where language itself speaks—sometimes in slips, sometimes in faulty instructions that open the Real within the Symbolic. In this particular sequence, a casual “please” becomes a keyhole into Borromean structures, grammar’s misfires, and the paradox of desire. What follows begins with the spark: an email dated 27 June 2025.
On Fri, Jun 27, 2025 at 8:47 AM Iraj Esmaeilpour Ghoochani <[email protected]> wrote:
Good morning Sir,
Happy to see that our spooky cowriting works as always. I have to read this again to be able to reflect but of course that you can share our correspondences. It is IT (ES=S) that talks, haha.
Hugs
Iraj
P.S. you know that 0.999…=1, do you? Check for proof if yiu do not.
Donald Kunze <[email protected]> schrieb am Fr., 27. Juni 2025, 14:03:
Hi Brother, Again, you vivify a whole new line of thought and keep our sessions going. I think you have found your perfect fan-club. I was playing with her please / please her. ON ACCOUNT OF ITS GRAMMAR, it points to the induction puzzle.
An Irish friend gave a talk years ago, after the financial crisis in Ireland, and showed some of the “for sale” adds placed in newspapers. One was “Skeepdog for sale.” Obviously a spelling error (“sheepdog”>”skeepdog”) but this particular one pointed to the moment of intense sadness when, having to part with a beloved pet, the owner’s finger had slipped from the “h” to the “k”.
Vergil makes a similar observation when he gets to Cumæ to descend into Hades to talk with Anchises. He suggests that while Dædalus was fashioning the doors he wanted to donate in thanks to the shrine, his hand had faltered. I’ve never seen any commentary on this, but it would mean that the tiles on the door had something wrong with them, due to Dædalus’s sadness over the loss of his son.
So, maybe in the eight panels depicting the story of Minos and the Minotaur and Labyrinth, a moment of emotion had made him make a mistake, and this is the “unconscious tic” that, as with the murderer in Young and Innocent, gave away some key connection.
This would be the REAL inside the Symbolic, at a “moment” where there is self-intersection and non-orientation.
Other cases: “I do not drink … wine,” Count Dracula’s short pause as he corrects the instruction to have a glass of wine at a dinner party.
I would suggest that “Colorless green ideas sleep furiously” is a less obvious but equally compelling case of the Real’s “haunting” of the Symbolic, as an ACT that slows things down or speeds them up, as in the case of the “No!” that comes too quickly in response to some suggestion.
Symbolic and Real, the Jekyll and Hyde … always using grammar to communicate, but by means of the faulty instruction!!!!
This would mean that EVERY instance of the Symbolic has at least the possibility/threat of such invasion, and that the invasion will lead to a case of faulty instruction, … “her … please”. The ERROR is critical, or should I say, the “EROR.” Colorless green ideas are faulty instructions until they come out into the sunshine (the perfect memory of Freud’s parapraxis).
As you put it, this potentiality is present even in the smallest unit of signification, the “plea” which is the demand to the Other, an appeal to the desire of the Other (unknown).
If “please” is a shortened form of “If it pleases you,” the “if” “it” and “you” are all variables. IF: in what instances and conditions? IT: what are we talking about? My frame means that I have a different view from the Other. YOU: the Other is a double construct. It is what is missing in the Other, fashioned by me into a temporary working model, a model that is missing something (that the Other desires). These three unknowns, X, Y, and Z, are all interactive. Like the three forms of negation, Verneinung, Verleugnung, and Ververfung, they have a Borromean structure. We do not know which comes first, last, or the middle, but thanks to NOT KNOWING the knot holds together.
The knot INSTRUCTS (“Stay tight!”), but the instruction is faulty (none of the rings actually link directly).
Dirac’s belt also instructs. One twist should be undone by a single twist, but it takes two twists!!! This is ALSO a FAULTY INSTRUCTION. My friend, we are “on the way to the bank”
“Her please!” —I can select “her” who is offered by the Other and say “please,” in hopes that the Other’s desire will coincide with my choice. or … —I can refer to the please that she had herself used in relation to a similar claim to the Other. Her “please” was more persuading than “mine.” Either way, context (narrative order) has justified the “plea” which is to clarify the “please.”
Please is specifically important because of the doubling of negation: (1) I do not know what you want, so I must make a case for getting your approval; (2) I do not know even what I myself want, so my case is complicated at the level of both evidence (it is undetermined whether or not there is a crime) and legal standing (I cannot establish what my relationship is to this “missing evidence”). Verneinung: “I do not have what I want, I must ask the Other.” Verleugnung: “The Other, over there, has control over getting this missing thing, it is not available to me over here.” Ververfung: Only if the Other should recognize and verify my lack/loss can this be remedied; in other words, hah hah, the Other is in a “double bind.” The Other not only does not know who I am or what I am asking, it does not who IT is with respect to these two missing pieces of information. THIS IS THE OTHER I CONSTRUCT (topologically) to deal with my demand, my please!
Because “please” attenuates “If it pleases you,” it is always a case of the subjunctive, the “if.” It proposes a future moment of the accord, between what was wished and what was done. THAT’S IT! But, we know that desire is self-perpetuating. It is always a case of THAT’S NOT IT! So, structurally, our plea is going to be a faulty instruction. It presupposes something will happen but this something is structurally impossible. The “it” will never be the “it” that is wished for. There will never be a coincidence, as there is in cases of need, between lack and non-lack, because lack is self-constructing.
We can see the “please” in action in the Three Prisoners’ Dilemma, with the two moments of paralysis (time of the gaze, time for comprehending) and the Act, the time to conclude. Although rushing out of the room simultaneously as all three claim the prize, this negates the instruction given by the warden, that they were in a contest where ONE would win who could conclude the puzzle. The ONE is really the answer, the “1” constituted by comprehension, where the Being of Truth connects to the Being of Knowledge.
In other words, the “1” is a faulty instruction. It may look like a number but in fact it is
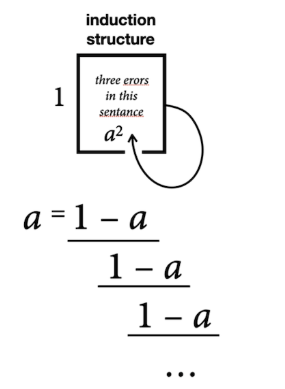
The faulty instruction (“=”) is that the answer will never cease to be given, although the “=” requests a single exchange, a return answer to the “please” of the “a.”
What can we do with the three-fold, Borromeo knot of negation?
Lacan: “Everything!!”
PS can I share this conjecture with the others?
The Hidden Door: Between Induction and Recursion
I wish to take up Don’s closing provocation and figure — not simply as a mathematical aside, but as a hinge opening a hidden door between induction and recursion, between the revealed and the occluded:
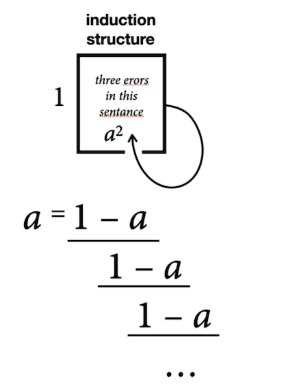
What you see above is the recursive formula of the φ number. Before going deeper into this let me ask what we are expected to confront in the next few pages:
”Why do we always speak of the golden ratio φ and almost never of its twin φ′?”
Now you may ask what the hell is φ′? Let me explain step by step.
Step 1: The given formula
We have the expression:
This is an infinite continued fraction or nested fraction. Let’s denote this infinite expression as itself, which expresses a fixed point or self-similarity in the equation.
Step 2: Simplify the infinite nested fraction
Since the expression repeats infinitely, the denominator at every level is also equal to :
This is because the nested denominator is again the same expression .
Multiply both sides by :
or
Rearranging terms:
Step 3: Interpretation
The infinite nesting in the formula expresses a self-referential equation, where the value depends on itself through an infinite descent.
This self-similar structure naturally encodes a fixed point of a function or an equation.
The quadratic equation emerges directly as the algebraic expression of this fixed point.
Step 4: Contextual significance
The image also mentions an “induction structure,” which corresponds to this kind of recursive definition or fixed point equation. This is conceptually aligned with many topological and algebraic structures where self-reference or recursion defines the object.
Formally, this infinite continued fraction expresses a function , where is a fixed point: . Solving this equation yields the same quadratic relation.
Mathematical note on the roots
Solving
gives
where the positive root relates to the golden ratio conjugate, showing that this infinite continued fraction encodes the golden ratio’s arithmetic at a deep, recursive level.
Commentary with mathematical insight
The roots relate closely to the golden ratio , and its conjugate .
Notice that
which is often called the silver ratio conjugate or the reciprocal of the golden ratio:
This is a number with fascinating algebraic and topological properties. Its continued fraction expansion is infinite and periodic, a signature of quadratic irrationals.
The equation
can be rearranged as
which already hints at recursive and self-similar structures: applying the function repeatedly leads to sequences governed by the golden ratio’s algebraic essence.
Alright — now, let us step into the neglected side, the shadow of the golden ratio, sometimes called :
The Anti-Number of Harmony and Growth
Most people worship because it appears in spirals, shells, and classical proportions. Its conjugate is treated like an unwanted twin — yet it holds a strange, inverted beauty. It satisfies the same quadratic relation as :
but where grows under iteration, shrinks and alternates sign:
It is the negative mirror in which growth becomes decay, expansion becomes oscillation.
The golden ratio obeys:
For the conjugate:
is still valid, but every step of the recursion flips the sign — a symbolic “yes/no” alternation. You could say represents a self-similarity under negation and its orientation changes each time you return.
While is linked to the Fibonacci sequence by:
its conjugate appears in the exact formula:
Here, is like the spectral term: its powers fade toward zero, but without it, the integers would never appear perfectly. It’s the subtractive whisper that makes the melody whole.
If is the Imaginary ideal — perfect proportion, endless projection — is the Real remainder, the term that resists being seen but makes exactness possible. It oscillates: plus, minus, plus, minus — like the signifying chain brushing against the void. Its magnitude is less than 1, so it never escapes the gravitational pull of zero. It is a number condemned to approach nothingness forever, yet by doing so, it anchors the beauty of its celebrated sibling.
To “meet” is to meet the side of proportion that refuses to stand in the light — the negative mirror image without which the golden ratio would be just an approximation, not a truth. It is the mathematical embodiment of what Borges might call “the other tiger,” and what in Sufi thought might be the bāṭin (باطن) — the hidden, inner truth, without which the ẓāhir (ظاهر), the outward form, collapses.
Now there is a deep connection between this graphs and the inversion in . This connection is not just a numerical curiosity here, it is structural to what the golden ratio and its conjugate are.
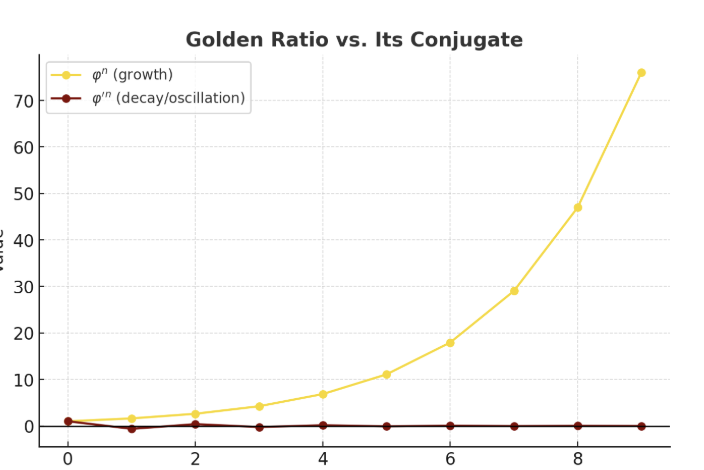
Here’s the visual: The golden ratio’s powers (gold) diverge smoothly, while φ′’s powers (dark red) oscillate and decay toward zero. the golden ratio’s powers (gold) soar upward in smooth growth, while its conjugate (dark red) oscillates in sign and collapses toward zero —one rising to infinity, the other spiraling inward to the void.
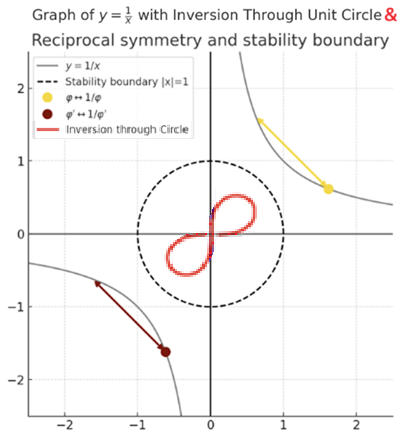
The graph of Metametaphor or the Unary Trait: The graph of is shown together with its inversion through the unit circle, marking the critical stability boundary . Outside this circle, points on the reciprocal curve exchange positions across the diagonal ; inversion draws them inside the unit boundary, compressing infinity into proximity and proximity into distance.
This oblique figure-eight is not simply a miniature copy but a reframed geometry: the act of inversion shifts axes, distorts angles, and inverts the very scale on which “stability” is measured. What was unbounded becomes bounded, but with a twist that preserves the algebraic structure while altering its metric visibility. Then, this is a way to read “dis-continuity” as a continious knot. The yellow and red points indicate reciprocal pairs and , while tracing how the outer hyperbola folds into a rotated lemniscate within the unit circle we remember that . To realize this let us superimpose y=1/x (the blue trajectory) on y=-1/x (the red trajectory) on the same ccordinates:
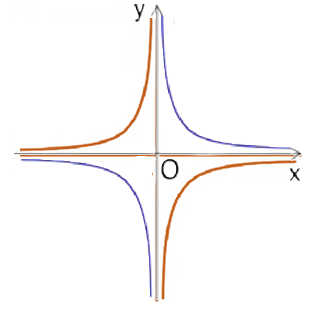
The minus sign in ϕ′=−1/ϕ is not just a sign, it is a rotation encoding the fundamental inversion of perspective. The graph y=−1/x is the image of y=1/x under this 90° rotation (when viewed complex analytically). The graph y=1/x lives on quadrants I and III; however, the graph y=−1/x lives on quadrants II and IV. They are mirror images under rotation by 90° about the origin.
(−φ,φ’) (φ,φ’) (φ’,φ) (-φ’,φ)
(−φ,−φ’) (φ,−φ’)
(φ’,-φ) (-φ’,-φ)
The intersection with the line y=x and y =-x knowing that ϕϕ′=-1 marks eight points of (−φ,φ’),(φ,φ’),(−φ,-φ’),(φ,-φ’),(φ,φ’),(-φ,φ’),(φ,-φ’)and(φ,-φ’)′; These in turn mark two intersecting rectangulars. This is the intersecting point of a hyperdimensional imaginary axis: the metametaphor axis of duality, inversion, and rotation depicted before in the form of two triangles. Now these two triangles are folded up into two rectangles. This reveals the hidden another metaphor axis as the orthogonal complement, where the unary trait’s paradoxes of continuity and rupture are resolved into a topological knot.
This topological knot is introduced through a hidden imaginary plane. I explain; actually the key insight is: the minus sign corresponds to a 90° rotation combined with inversion.
In fact, if you define the map :
then
which can be read as a composition of inversion and a 90° rotation (multiplying by ) twice (since ).
More directly: The inversion exchanges the inside and outside of the unit circle. Why? Because φ and φ’ satisfy the inversion formula: φ.|φ’|=1 (r.r; where r=1).
Definition: Metametaphor is an operator that acts a 90° rotation combined with inversion.
Metametaphore transforms growth into decay, continuity into rupture, and revealing the hidden dynamic axis orthogonal to the visible one. Psychoanalysis is a metametaphor operator: It manifests the dynamic where every expansive movement is counterbalanced by a contractive oscillation, constituting the binary pulse of the psychic life: extended without knowing of it. metametaphor is the “operator of symbolic difference”—not simply difference of meaning, but difference of orientation and topology. In the next pages I will try to give a clinical example of this operator throgh that significant objects or situations in clinical contexts, like a beetle in Mr. E’s panic attack. Such objects are are linked to important events primarily through their phonological form rather than their meaning. This is how metametaphor works: out of the domain of meaning but changes the meaning insideoutsidely after the operation is done, that is after the “Que faire?” is turned into Käffer and through this loophole, what was pathologically frighthening causing thrembling turned into a dampable Thing: a controllable insect. Between these two lies a hidden space that much like the imaginary domain in mathematics which is corelated to the Real in Lacan’s psychoanalysis. In this case, the phonological form “Käfer” is associated with the indecisiveness of Mr. E’s mother regarding her marriage to his father, encapsulated in the phrase “Que faire?”
The Golden Ratio as a Fixed Point of Inversion-Shift
The defining equation for is:
If you strip away the “+1” for a moment, the core is:
The graph performs a hyperbolic inversion:
Large numbers become small, small become large.
The “+1” in the formula for is a translation along the x-axis before the inversion. This makes the unique fixed point of the composition:
i.e.,
So both and are equilibrium points under a Möbius-like transformation that contains inversion at its heart.
Positive vs. Negative Branches of the Hyperbola
The equation has two disconnected branches:
Quadrants I & III: (or both negative, moving together)
Quadrants II & IV: (or signs alternating in iteration)
lives on the positive-growth branch, lives on the negative-decay branch.
The fact that means iterating pushes it away from itself toward infinity, but when composed with “+1” it becomes stable. Topologically, they are the two fixed points on opposite lobes of the same hyperbola. Not FINISHED!
Left: the inversion project manifesto
Oscillation and Inversive Symmetry
Iterating alone:
If , you stay positive.
If , you stay negative. No oscillation.
But iterating :
If you start with , you oscillate sign when you subtract 1 and invert.
This creates a sign-flip inversion: a “hidden half-twist.”
This half-twist is why alternates between positive and negative powers: it’s a numeric strip, linking infinity and zero by inversion.
is like the barred signifier: the point at infinity is bound to the origin by inversion, mirroring the impossibility of closure in the signifying chain.
is the Imaginary/Symbolic fix-cross-point: stable, harmonious, on the visible branch.
is the Real fix-point: hidden, oscillating in itself, yet structurally necessary for the first to exist.
Dr. Hyde and Mr. Jekyll as and
: radiant, expanding, the “classical” proportional ideal — the Jekyll of harmony. It grows under iteration, its image is self-similar. : the shadow twin, negative and contracting, the Hyde that oscillates signs as it collapses toward zero. Both satisfy the same equation:
which means they are fixed points of a transformation containing inversion at its heart. But they are structurally coupled — you cannot write the exact Fibonacci sequence without lurking in the formula. It is literally the spectral term that makes the integers exact, like the slip of the “h” to “k” in skeepdog, the unconscious tic of Daedalus’s hand.
Now we are talking about the metaphor whose whatness we will never know but we tend to it via its formula that carries this mysterious 1/x in its heart:
captures this dynamic of replacement if “h” for “k” by introducing a cut: a void held together by a “symmetrical difference” (the inversion of the signifier suppressed by , that allows Lacan to appear to “cancel out the two primes). The or x is the unknown signification. the whole formula reads: the signifying function of the substitution of one signifier for another is congruent with the crossing of the bar. Again, Lacan’s metaphor formula
encodes the structural process by which one signifier substitutes another signifier on the chain, producing a new signified effect in the sense that a Word becomes so loaded with the meaning of meaning (the omited that holds its trace in a secret closed circuit made of divergence of repetion and convergence of suppression[1]) that it it takes the features of Flesh (signified): This is the meaning of crossing the bar that isolates signifier from the signified. Now the bar is appropriated inside the metaphore as a function:
By this operation, Lacan cancels out the two appearances of in the formula, reflecting the topological idea of folding or identifying points, such that the substitution folds out of the chain, but its trace remains. The resulting expression, , indicates that the new signifier functions on an inverted or transformed domain, (or 1/x), emphasizing that metaphor produces a new meaning by folding one signifier into another through this cut and inversion.
Lacan’s metaphor formula embodies a structural rupture—a cut—that enacts a substitution that inverts and folds signifiers onto one another, generating a new signified through a dynamic interplay of absence and presence. The “symmetrical difference” is the algebraic expression of this inversion, allowing Lacan to conceptualize metaphor as a non-trivial topological transformation rather than a mere linguistic replacement. Back to Don.’s example:
An Irish friend gave a talk years ago, after the financial crisis in Ireland, and showed some of the “for sale” adds placed in newspapers. One was “Skeepdog for sale.” Obviously a spelling error (“sheepdog”>”skeepdog”) but this particular one pointed to the moment of intense sadness when, having to part with a beloved pet, the owner’s finger had slipped from the “h” to the “k”.
If we listen analytically, the slip is not accidental. It’s a precise cut — an inversion in the chain of signifiers. The “h”→“k” switch is not about a mere letter replacement; it’s about a structural pivot that works like the transformation x = 1 + 1/x. In this equation, the number φ (the golden ratio) is a fixed point — a number that, when inverted and added to 1, reproduces itself.
But here’s the key: you cannot write the exact Fibonacci sequence without φ′ (its conjugate, φ minus one), the spectral shadow, present in the formula. This φ′ is not directly “there” in the conscious material, just as the patient never consciously thinks of “k” as haunting “h.” Yet it is structurally indispensable. Lacan’s metaphor schema
shows how M (a master signifier, here “Sheepdog”) replaces another signifier S′ in the chain, producing a new signified through the unknown x. The “h”→“k” cut is the crossing of the bar adding a surplus to the meaning of the original signifier in the sense of a flesh (a lost signified). The result is that “Skeepdog” now becomes more than the original pet: it condenses hidden traits, forbidden jokes, or early affective traces. It is overloaded with “the meaning of meaning” — the omitted S′ holding its trace like a loop of suppressed repetition and converging suppression. The altered signifier takes on a quasi-fleshly quality, almost palpable in the way the patient smiles when speaking it.
In clinical structure, the hinge between induction and recursion is often no more than the flick of a phoneme, a minimal displacement on the axis of the signifier that precipitates a total reconfiguration of meaning. Freud’s patient, for whom Käfer (“beetle”) unconsciously condensed Que faire? (“What to do?”), traversed this hinge without crossing any semantic bridge — the sound alone enacted the pivot. Lacan formalizes such operations in his formula of metaphor, S (S’/S) → S+, where the substitution of one signifier for another generates a surplus of meaning. In our example, Käfer occupies φ, the “golden” fixed point in the chain, while its conjugate φ′ (Que faire?) inverts its function: one form opens the question, the other hides it in insect form. Similarly, in Gestapo → “gest a po,” Lacan shows how a chain can break at a purely phonological seam, reentering the structure with a displaced signification that no longer aligns with its historical referent. This is not metaphor as decoration, but as structural recursion: the chain folds upon itself, the missing element (the sadness of departure from a dear pet: Sheepdog) returns under another name= Skeepdog, and meaning reemerges as the conjugate of its own erasure.
Why this is 1/x
Metaphor, in this clinical frame, appropriates the 1/x structure: The overt signifier M (“Sheepdog”) is stable, but the transformation inverts something hidden (h→k, φ→φ′), which is structurally necessary for the stability to appear.
Just as 1/x flips numerator and denominator, the unconscious flip inverts presence and absence: the absent trace (φ′, the lost “h”) is what lets the present form (“Skeepdog”) stand.
The new signifier is thus a fixed point of an inversion — a golden ratio of speech — where the original and its shadow remain bound in a spectral equation the patient will never fully “solve,” but will circle around in dreams, slips, and metaphors.
and the Formula of Metaphor
Lacan’s next formula for metaphor:
has the structure of substitution and inversion: the “horizontal” relation between signifiers hides a “vertical” leap in meaning. The transformation is an exact numeric analogue:
It flips large and small, subject and predicate, the “frame” and “content” and in the case of “Please!”: verb and adverb. The fixed points and are like two “meanings” stabilized in different registers: one positive, one negative, each locked to the other through the same law.
In metaphor, the substitution is never perfectly symmetrical — meaning is deferred, twisted, often through a faulty instruction in the chain. In , that same fault shows up as a sign inversion when you iterate .
The Fibonacci Slide-Rule and Lacan’s φ′ Oscillation
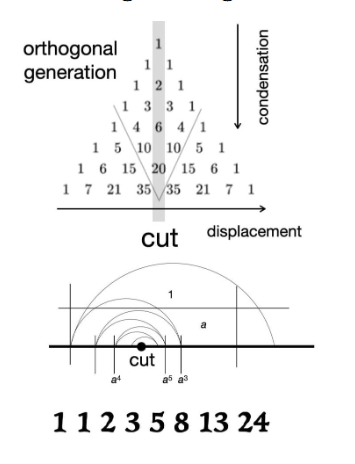This image beautifully visualizes Lacan’s use of the Fibonacci sequence and the “slide-rule analogy” to explain the operation of metaphor as a dynamic structural process, pivoting on the interplay between the golden ratio (φ) and its conjugate (φ′). Phi Prime (φ′) as the Hidden Oscillator: The conjugate golden ratio (φ′), often neglected in popular discourse, here plays a regulatory role—it enforces a toggle mechanism. The sequence alternates around φ, ensuring that the symbolic system never collapses into linearity but remains caught in a dynamic loop of deferral and return (similar to the metaphor’s displacement of one signifier for another). the inversion project manifesto
The Fibonacci sequence shown in the image, generated through orthogonal operations (Pascal’s triangle) and condensed into a spiral, is more than mere number play—it encodes the symbolic economy of Lacanian signification through alternating toggles around a fixed point. This fixed point corresponds structurally to φ = (1 + √5)/2, the golden ratio, which serves as an attractor or equilibrium in recursive symbolic processes.
The “cut” in the image marks a topological rupture in the signifying chain where Lacan’s metaphor operates. The slide rule analogy embodies this: as the ruler slides forward, numbers representing symbolic elements “tick” alternately back and forth, reflecting the conjugate ratio φ′ = (1 – √5)/2, the spectral counterpart of φ. This conjugate ratio functions like a “hidden regulator,” pulling the sequence not toward unbounded growth but maintaining it in a bounded oscillation—a constant negotiation between presence and absence, signifier and barred signified. Lacan’s Slide Rule is a Model of Metaphor: The sliding ruler’s movement encodes metaphor’s logic: the substitution of one signifier (S′) for another (S) is not a simple replacement but an oscillation, an ongoing back-and-forth across the symbolic cut, structured by the interplay of φ and φ′. The embodiment of φ with its conjugate (φ′) is already readable inside the Fibonacci numbers grow according to the recursive relation , which can be solved exactly with Binet’s formula:
Here, the term is the spectral conjugate, encoding the hidden oscillation around the fixed point φ.
Now, Lacan’s metaphor formula:
can be read as a symbolic analogue of this oscillation: the substitution (slide) around the barred signifier (cut) produces a new signified that emerges only through this alternating toggle (embodied by ).
As for clinical and theoretical implications, like Freud’s Käfer turning into Que faire?, or Lacan’s Gestapo phonological slip, the metaphor toggles between forms, never settling fully, caught in the topological feedback loop visited by the Fibonacci slide-rule.
Now, the word/sentence “please” — whether “If it please you” (subjunctive, appeal to the Other) or “Please me!” (imperative, demand) — lives in the same slide-rule of reversal:
The demand to the Other always loops back through an embeded lack. The “it” in “If it please you” is unknown and unknowable — the variable in a faulty instruction.
Structurally, we have three variables (IF, IT, YOU) — X, Y, Z — knotted Borromean-style like Verneinung, Verleugnung, Verwerfung: remove one and the others collapse. This is the same as the fixed points of the Möbius map : Remove the negative branch () and the positive branch loses exactness. Remove the positive () and the shadow becomes a meaningless oscillation.
Conclusion: Faulty Instructions as the Real Ins(l)ide the Symbolic
The slip in skeepdog, the misplaced tile in Daedalus’s gate, the pause in “I do not drink … wine,” the Chomskyan “Colorless green ideas sleep furiously” — these are all the Real’s inf(l)ection inside the Symbolic. They happen at points of self-intersection and non-orientation: moments when the signifying chain performs a half-twist.
That half-twist is exactly what experiences under iteration: its sign alternates — the Möbius path is felt as reversal, not as smooth progression.
So: “please” is structurally -like — it never reaches the harmonious closure of . It loops, flips, and returns with the remainder still intact. It is always “If it please you” and “please me” at once — and the oscillation is the Real’s shadow running alongside the Symbolic.
Again, the word “Please” in Please Me (and Read This) — If It Pleases You is rather like φ and its shadow root: one expands, the other contracts. Desire lives in their ratio.
-
Check: Don. Kunze ]Video[ (2023) Generating the Torus: How the Torus Void(s) Become Lacan’s Formula for Metaphor; URL: Generating the Torus: How the Torus Void(s) Become Lacan’s Formula for Metaphor
“This silent video begins with the idea of the torus generated by a “figure” trying to complete its circuit while the “ground” moves behind it. The inability to complete the circle/circuit creates a gap, ‘a’, that relates the two voids of the torus. This in turn is the model of the relation of the aim and goal in relation to the RIM Lacan describes in Seminar XI.” ↑