The point is…

Iraj E. Ghoochani

This is one of the first texts written for the project ‘The Point Is…,’ a visual philosophical endeavor that I hope to collaborate on with Claudio Sagribi in 2025, or whenever The Point reveals some of its hidden features to us.

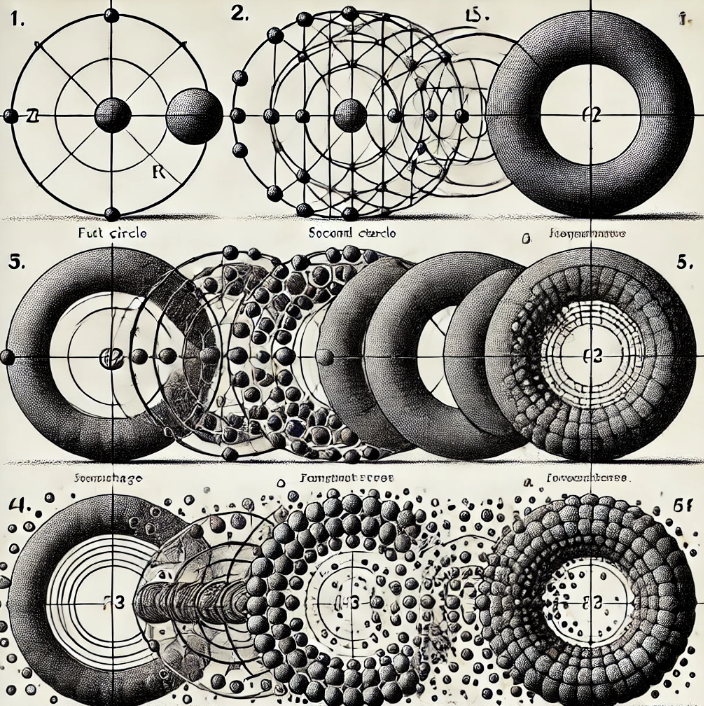
We begin with a circle of radius R. Its circumference is 2πR. Imagine twisting or transforming this circle in such a way that it forms two smaller circles. These two new circles have radii r1​ and r2​, and their circumferences are 2πr1 and 2πr2, respectively. The relationship between these circles is such that the sum of their circumferences equals the circumference of the original circle, i.e.,

2πR=2πr1+2πr2=2π(r1+r2)

• R=r1+r2

in the illustration, the ratio ρ=r1/r2 between the radii of the two smaller circles inside the larger circle is 1, meaning r1=r2​. This equality ensures that the two smaller circles are identical in size, which creates a symmetrical and balanced configuration at each step of the process. Each step in this recursive process maintains this symmetry, leading to a self-similar pattern where the circles within each larger circle are identical in size. This kind of pattern is reminiscent of fractals, where the same structure repeats at smaller and smaller scales, and each smaller part is a miniature replica of the whole. We can practically use any value for the ratio ρ=r1/r2, allowing the sizes of the smaller circles to vary relative to each other. When ρ=1, however, the two smaller circles are identical, resulting in a symmetric pattern and a faster convergence to our conclusion:

…

Iterative Process: Continuing this process—taking each of these circles and further twisting or dividing them into more circles, where at each step, the sum of the circumferences (or equivalently, the sum of the radii) remains constant.

Limit to a Line: As this process continues, with the circles becoming increasingly smaller and numerous, they propose an intriguing limit: the final configuration would be a line made of centers. In this line, every point could be seen as a double, representing an interesting feature of the point: The point harbors a subtle, hidden movement—a silent spin—where the point itself embodies the spin, representing both a return to and a transformation into its own hollow center as its origin:

There is still another way of looking at the nature of a line as the sum of infinite points, especially when viewed through the lens of a circle.

Reinterpreting a Line as a Circle Viewed from the Side

The equation of a circle in the Cartesian plane is

where r is the radius of the circle. This equation represents all the points (x,y) that are equidistant from the origin.Now if you imagine looking at this circle from the side, you would only see the x-axis. The y-dimension collapses in this view, but the points still exist in a certain abstract sense.

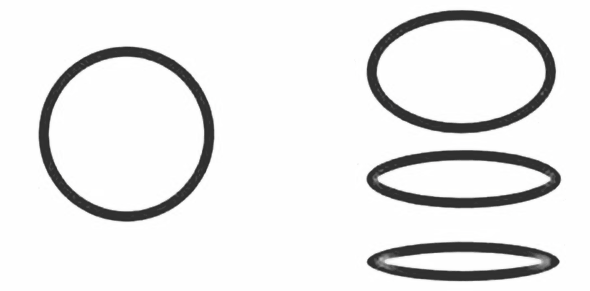
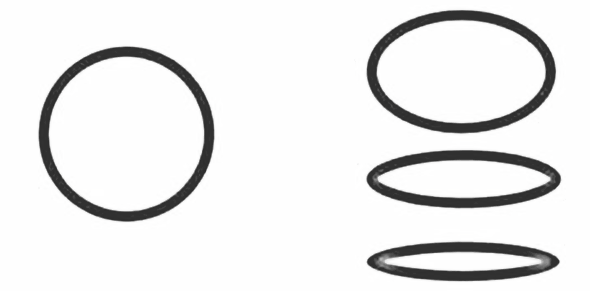
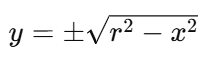The line is a circle looked at from the side, you’re suggesting that each point on the line represents two potential points on the original circle: one for the positive y value and one for the negative y value. Mathematically, this corresponds to the fact that for any given x on the circle, there are two corresponding y values:

Whenever we collapse a circle to the x-axis (viewed from the side), every point on the line can be thought of as representing two points: one where y is positive and one where y is negative. This gives us again a fascinating interpretation: each point on the line is “double-pointed,” harboring both an outgoing and returning direction. The point is the spin.

This dual nature can be seen as a metaphor for the orthogonality inherent in nature. When considering the first scenario—collapsing tangent circles by shrinking them until they converge at their origins—the orthogonality is represented by the twist of the circles. Conversely, in the second scenario—collapsing a circle to the x-axis (viewed from the side)—the orthogonality is reflected in the twist of the entire coordinate plane.

Visualizing the Concept

This duality could remind us of quantum superposition, where a particle can exist in two states simultaneously until observed. Similarly, every point on the line could be seen as representing two states collapsed on one position: The point.