The Loophole at the Origin: On x = 1/y, Nested Tori, and the Blindness of Continuity
Iraj E. Ghoochani
Abstract:
This essay explores the topological, psychoanalytic, and poetic implications of the reciprocal function x=1/y. Drawing from Lacanian topology, projective geometry, and metaphorical logic, we investigate how singularity at the origin conceals a double rupture. Through a comparative reading of linked tori and the trefoil knot, and inspired by a parable of theft hidden in “plain sight”, we propose that y=1/x (equally could be written as x=1/y) encodes a Möbius structure of the subject. hrough a comparative reading of linked tori and the trefoil knot, and inspired by a parable of theft hidden in plain sight, we propose that encodes a Möbius structure of the subject. his exploration suggests that the singularity (the rupture or discontinuity) is not a fixed category but a structural position that rotates among the three Borromean registers—Symbolic, Imaginary, and Real. At each structural turn, one register takes on the role of discontinuity, while the other two function as reciprocal, ontologically equivalent fields. It is not a matter of hierarchy, but of topological turning.
The Parable of the Wheelbarrow
A man smuggles wheelbarrows across a border. Each day, guards inspect the contents of the cart, never suspecting the cart itself is the object being stolen. This is the key to our argument: what appears most visible often conceals its own rupture. The structure is what passes unseen, precisely because we look too closely at its contents.
This parable sets the tone for understanding singularities in functions like y=1/x. The origin appears to be the site of a single rupture; in fact, it hides a dual blind spot. Each axis conceals a cut in the other. Like the wheelbarrow, the rupture is in the form itself.
Now, the reciprocal function appears smooth along each axis except at the origin. If we mirror the graph across the line y=x, it becomes, and now the rupture has moved: what looked continuous along is now broken at . The origin thus holds not one singularity, but two—a crossed structure of blindness.
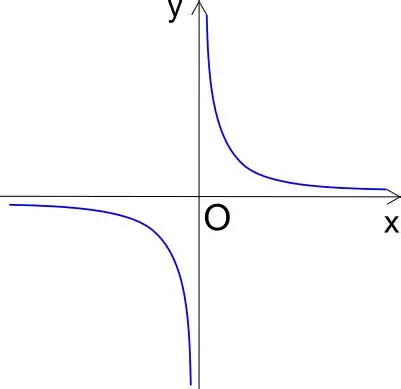
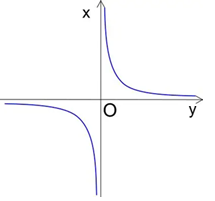
Left: y=1/x— The x-axis appears continuous, ruptured only at x=0; Right: x=1/y — the mirror image across the line y=x, where now the y-axis appears smooth, except at y=0. Both interpretations are true: each axis serves as the illusion of continuity while concealing its own singular rupture. The act of flipping the graph reveals that the function’s structural blindness lies not in its visible discontinuity, but in the axis we take as ground. Like the wheelbarrow in the parable, the rupture hides in the form that supports everything else.
This moment is anamorphic: the singularity changes its form depending on our orientation. The smoothness of the curve is a seduction, a demand for coherence. But beneath it lies a double cut. The graph conceals its structure in the name of its continuity.
Lacan’s Irreducible Origin
As Lacan notes in Seminar XII: “The origin in Cartesian space is not reachable—it is that which remains excluded by the very coordinates it structures.” It is the point where symbolic coordinates fail. It is not merely absent; it is structurally excluded. This irreducibility becomes formalized in the Möbius topology of the subject: the twist that joins the Symbolic and the Imaginary from a single surface. In Darmon’s reading[1], the Real is similarly the cut that makes the Möbius band possible—an irreducible twist that joins and separates.
When we conceive the x and y axes as circles of infinite radius, Cartesian space becomes a toroidal topology. Each axis folds into itself, creating two structural holes. This transforms the origin into a knot of passage: not a coordinate, but a recursive crossing of two loops.
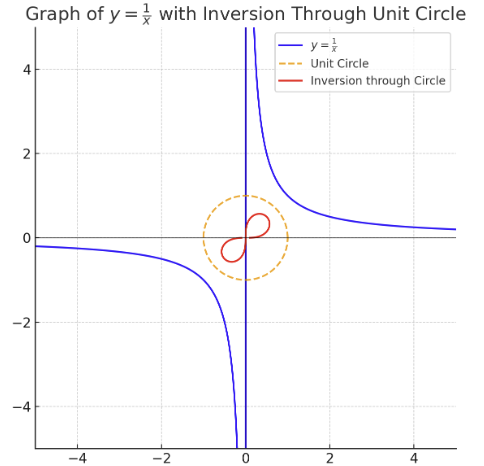
In this reading, the function becomes not a broken line, but a figure-eight traversal across the torus. This figure-eight, or oblique infinity sign, becomes especially visible when we inscribe a unit circle at the center: the function intersects this circle in four symmetrical approaches to the origin, one from each quadrant. The four infinities of the hyperbola mirror each other through the center, revealing the singularity not as a point of rupture but as the focal convergence of a rotational topology. The discontinuity is an illusion born of affine limits.
Nested Tori: Reciprocity and Blindness
In a more complex configuration, each axis can be imagined as a torus passing through the hole of the other. This yields a model of reciprocal voiding:

Linked Tori — two interpenetrating loops, each threading the void of the other, representing the mutual blindness of dual structures like y and x , or signifier and signified or Word and Flesh. The x torus passes through the y torus’s hole and the y torus passes through the x torus’s hole.
This double-nested system represents mutual definition through absence. Neither structure exists in isolation. Each lives inside the blind spot of the other. The structure becomes a Hopf link—a minimal linkage of two loops. Or, from another angle, a trefoil knot: a self-entangled topology representing irreducible subjectivity.

The Trefoil Knot — a single, self-entangled curve modeling the recursive torsion of the subject and the irreducible singularity at the origin.
Both the Trefoil Knot and the Linked Tori frame as both reciprocal and inherently knotted. Now, this topological reading suggests an answer. The Symbolic and Imaginary are linked loops, folding and reflecting one another. But the Real is the cut: the Möbius twist that makes their junction possible. However, rather than treating them as equal ontological registers, one might propose a rotational Borromean logic, in which any one of the three can cyclically assume the role of structural discontinuity. At each turn, one ring becomes the void or rupture while the other two become reciprocal, ontologically equal fields. There is no top or bottom, no fixed axis of truth, only turning: the topology of subjectivity as recursive twist.To fully differentiate the Euclidean observational space of Cartesian diagrams from the topological space of the psyche, Don Kunze provides a crucial distinction:
“The L-schema is about how the Imaginary of the a–a’ axis (the Euclidean world in which the Analyst and Analysand live, work, see, and act) blocks the Unconscious, structured as Symbolic, from reaching its GOAL, which is the ES. […] It is not Euclidean because the trajectory of the Unconscious does not move in 3-space, it travels in topological 4π space (rotational space) […] where a CIRCUIT can be completed in 4π (like Dirac’s belt) but any projection will show it as 2π, requiring the representation to show a jog, crack, or other discontinuity where, in the Real of the unconscious, there is none.”
Kunze’s insight clarifies why singularities in y=1/x appear as ruptures in flat space. The Real isn’t missing; it is rotationally displaced. What seems like a discontinuity at the origin is in fact the twist required by the 4π logic of the unconscious. Like the Dirac belt, which cannot return to its original form after one full twist (2π), but only after two (4π), the unconscious completes circuits unseen in projection. The Möbius twist is not a flaw; it is a structural necessity: the law. As Freud famously wrote, “Psyche ist ausgedehnt, weiß nichts davon” (“The psyche is extended; it knows nothing of it”). This unnoticed extension, folded and topologically warped, aligns with the Möbius model: the unconscious circuit closes not in space, but in structure. This same topological law helps illuminate the structure of transference, or even metaphor itself—since every transference can be understood as a metaphor: a displacement across structural registers, linking disparate coordinates through a shared axis of absence. The function y=1/x, with its rotational blind spot and mirrored infinities, models this logic: the substitute appears coherent only by virtue of the cut it conceals.
Final Thought
Y= 1/x encodes more than a mathematical curve. It is a topological rebus, a psychoanalytic diagram, and a parable of structural blindness. The origin is not a point but a knot; the singularity is not a break but a twist. If the trefoil knot is the subject, and the linked tori are the axes of desire and identification, then the Möbius strip is the Real: the structural twist through which the Symbolic and Imaginary appear as mirror images, but never coincide.
- Marc Darmon, LES SCHEMAS R ET I from Essais sur la topologie lacanienne in reading seminar xiii: the object of psychoanalysis; URL: https://boundarylanguage.psu.edu/reading-seminar-xiii-the-object-of-psychoanalysis/ ↑