The Wife of Potiphar: The Fractal Path of Inversion Circles
Iraj E. Ghoochani
Fresh blows the wind
For home;
My Irish child,
Where do you tarry?
—Eliot quotes form Tristan und Isolde; Wasteland[1]
 The story of the wife of Potiphar reflects how desire spirals within the Big Other (the symbolic order). The Big Other, often represented as “A,” structures the subject’s world: She named everything after his name, Joseph. The Big Other determines what is possible and what is forbidden, operating within the domain of possibility (Joseph, a slave-like young footboy, was at her service). In the last article, we discussed the “near yet distant” structure of this machinery, which takes a demand and turns it into desire through its infinite loops and folds. Now, in this article, we explore a geometrical interpretation of this longing for desire and the structure of fantasy. Instead of using the golden ratio (phi, 1.618), we turn to a transcendental figure—the celebrated number pi—which reappears everywhere as the underlying truth behind reappearance itself.
The story of the wife of Potiphar reflects how desire spirals within the Big Other (the symbolic order). The Big Other, often represented as “A,” structures the subject’s world: She named everything after his name, Joseph. The Big Other determines what is possible and what is forbidden, operating within the domain of possibility (Joseph, a slave-like young footboy, was at her service). In the last article, we discussed the “near yet distant” structure of this machinery, which takes a demand and turns it into desire through its infinite loops and folds. Now, in this article, we explore a geometrical interpretation of this longing for desire and the structure of fantasy. Instead of using the golden ratio (phi, 1.618), we turn to a transcendental figure—the celebrated number pi—which reappears everywhere as the underlying truth behind reappearance itself.
Two key moment of video The Logic of Phantasy: Lacan’s Slide-Rule Analogy by Don. Kunze[2] In his seminar XIV on the logic of phantasy, Jacques Lacan makes two references to the now-obsolete calculating device known a the slide rule. First he says that the subject advancing toward the sexual act is not thinking of theory or, of that matter, of failure; but the fact remains that the law of pleasure involves the failure of jouissance and the common, quite common, experience of dissatisfaction. Later Lacan defends the slid-rule as a means of seeing the novelties in the structural order of phantasy, a means of ventilating theory and avoiding muddles. But, what does Lacan mean with his example of the slide-rule? … This video … does show what Lacan’s slide-rule is about and how it works in relation to the Fibonacci Golden ratio, which Lacan calls the “mean and extreme,” because it is something that happens inside an interval and outside as well. (ibid.)
Lacan’s exploration of the Fibonacci sequence captures the recursive nature of fantasy: Each number in the sequence is generated by the sum of the two preceding numbers, a process of continual becoming. This reflects Lacan’s notion that fantasy is both structured by and structures desire, perpetually renewed yet never reaching a final state of satisfaction. The mathematical representation of this, especially through phi, becomes more than just a numerical ratio—it embodies the gap between the subject’s desires and the ever-receding satisfaction of those desires. Lacan’s integration of the Fibonacci sequence and projective geometry into psychoanalysis speaks to a key insight: desire, like the Fibonacci spiral, is both infinite and self-similar. It is recursive and seeks fulfillment within the constraints of the symbolic but can never fully grasp it—there is always a beyond, a failure inscribed within the logic of satisfaction.
This recursive movement between satisfaction and failure ties into Lacan’s concept of the objet petit a, which represents the unattainable object of desire. This objet petit a is less than the Big Other_ in the sense of its nature as a postponed residue_ yet crucially defines the subject’s relation to the symbolic order. It is this gap, where the recursive and fractal nature of fantasy and desire resides. In Lacan’s metaphor of the slide rule, this movement oscillates between the odd and even iterations of objet petit a: mirroring an endless attempt for reconciling desire with the symbolic order; an attempt that is doomed to always fall short.
Φ vs. π; Algebraic vs. Transcendental
For good resons this article is aimed to change Φ for π. Before doing that let us start with the biggest difference that distances these two numbers.
The golden ratio, often represented by the Greek letter φ (approximately 1.618…), occupies a unique place in both mathematics and art. While its aesthetic significance is widely celebrated, its mathematical properties are equally intriguing. A crucial aspect of φ is its classification not as a transcendental number, but as an algebraic number. This distinction arises from the nature of the equations these types of numbers satisfy. Algebraic numbers are defined as numbers that are roots of polynomial equations with integer coefficients. The golden ratio is one such number, as it is a solution to the quadratic equation:
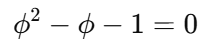
Solving this equation yields:
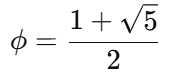
On the other hand, transcendental numbers are those that do not satisfy any polynomial equation with integer coefficients. Famous examples of transcendental numbers include π (pi) and e (Euler’s number), which resist such simplification. Therefore, while φ may possess a profound connection to natural forms and aesthetic proportions, it does not share the same transcendental status as π or e. Instead, φ finds its identity as a solution to an algebraic equation, deeply rooted in the structure of mathematics.
Now that we understand this essential difference, we can draw a parallel argumentation with Lacan, this time using π (pi), which further surprises us by introducing the unexpected concept of the inversion circle.
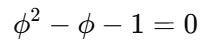 Algebraic Nature of φ: The golden ratio φ is algebraic, meaning it is a root of a polynomial equation with integer coefficients, specifically:
Algebraic Nature of φ: The golden ratio φ is algebraic, meaning it is a root of a polynomial equation with integer coefficients, specifically:
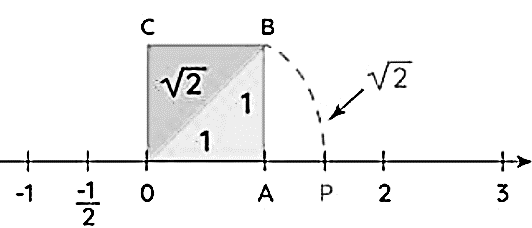
Transcendental Nature and Unattainability: Transcendence does not equate to unattainability. For instance, when you add a unit perpendicular to another, the triangle forms a hypotenuse of magnitude , which is non-integer, irrational, endless but still algebraic.
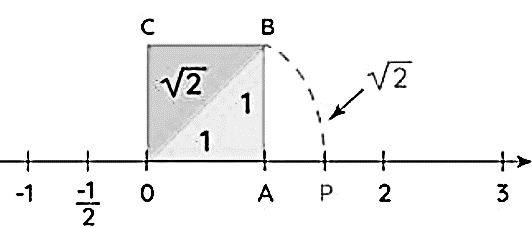
Modeling with π: π may offer a more fitting framework for exploring the relationship between the subject and the object, particularly the concept of the objet petit a. This is due to π’s transcendental nature and its fundamental role in circular geometry.
Circle and Orthogonality: A circle inherently embodies the notion of orthogonality, as the radius is always perpendicular to the tangent at any point on the circumference.

π and the Circle: A circle, a fundamental geometric shape, involves the transcendental number π. While π is not an algebraic root of any polynomial, it plays a crucial role in defining the circle’s properties and is considered “NP” (non-polynomial) in this context. NP problems involve complexities beyond polynomial-time solutions in computational theory.
Circumference and Transcendence: π is the ratio of the circumference of a circle to its diameter. For an integer radius of one, the circumference is 2π, revealing π’s transcendental nature with infinite decimal places: the whole Library of Babel resides in the decimals of the π including this article.
Integer and Transcendental Values: According to our analogy, integers, rational and even irrational numbers (for example represent the Symbolic order, while transcendental numbers represent the Real. The subject navigates the interplay between these realms within its fantasy.
Sliding Ruler Analogy: This is similar to the sliding ruler concept from Seminar XIV, but using π instead of φ. This approach reconstructs the model using the transcendental nature of π and gives us the opportunity to see the whole thing from the perspective of the inversion circle.
Circle Formula and Uncertainty: Consider the formula P=2πr. If r is an integer, P is transcendental, and vice versa. This can be interpreted as a circular analog of Heisenberg’s uncertainty principle. The essential nature of this limitation is reflected in the transcendental nature of π.
Twisting and Circles: For an integer value P (which corresponds to a transcendental r), joining the ends of P and twisting it results in two circles. The sum of their circumferences equals P: P=p1+p2.
Creating a Trefoil: These circles can be folded into a semi-trefoil knot, (by twisting it back onto itself (Lacan called it inverted 8 in session five of XIII)) as a foundational element of a torus.
P = p1 p2 =
P=p1+p2: We can express the total circumference P as P=p1+p2, where p1 and p2 are the circumferences of each circle.
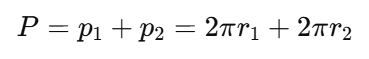 Combining with π: We can write
Combining with π: We can write
 or equivalently:
or equivalently:
This reveals an inversion circle concept governing integers and transcendental numbers. Why? Because we are free in our slide and there is a point in which one circle turns into the inversion circle of the two others:
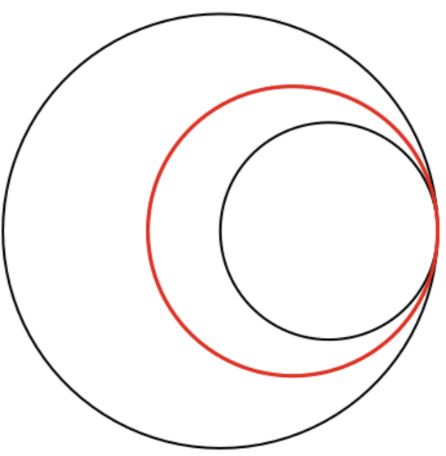 After sliding the original circle in its trefoil-like format, there is a moment in which one circle, the red circle above, turns into the inversion circle of the original circle and the smaller one. This visualization underscores the inversion circle concept as the hidden locus of interplay between circles as the same thing. Every circle is the same very thing: a locus for interplay between integers and transcendental numbers because their radiuses: P, the bigger original circle can be chosen to be an integer and p2, then the radius of all smaller circles take the transcendental feature of , akin to the relationship between A and the objet petit a in Lacanian psychoanalysis. Every single circle is the same and this goes down until it shrinks onto a single point. The point is a circle.
After sliding the original circle in its trefoil-like format, there is a moment in which one circle, the red circle above, turns into the inversion circle of the original circle and the smaller one. This visualization underscores the inversion circle concept as the hidden locus of interplay between circles as the same thing. Every circle is the same very thing: a locus for interplay between integers and transcendental numbers because their radiuses: P, the bigger original circle can be chosen to be an integer and p2, then the radius of all smaller circles take the transcendental feature of , akin to the relationship between A and the objet petit a in Lacanian psychoanalysis. Every single circle is the same and this goes down until it shrinks onto a single point. The point is a circle.
Algebraic vs. Transcendental: We began by contrasting ϕ, an algebraic number rooted in natural aesthetics and mathematical structure, with π, a transcendental number integral to the geometry of circles. While ϕ is a solution to a simple quadratic equation, π defies such algebraic constraints, symbolizing the unattainable yet ever-present Real in Lacanian terms. π is Real.
Inversion Circle and Orthogonality: The concept of the inversion circle emerged as a metaphor for the hidden connections, not only between the algebraic and transcendental, but also for mirroring many ethnotopological issues for example the relationship between law (Kant) and transgression (Sade). The algebraic ϕ and the transcendental π, when intersect through an orthogonal structure, their interaction will give rise to an inversion circle—a locus where in our ethnotopological plane, the Symbolic and the Real meet.
Recursive Shrinking and the ρ Factor: To deepen our understanding, we derived the value of ρ (the ratio between the radius of the next circle to the radius of the inversion circle) by examining the relationship between the radii of a sequence of circles. The value of ρ is determined by solving the equation:
![]()
![]()
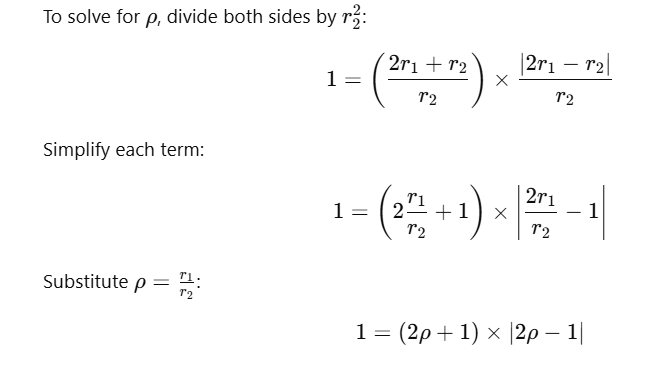
![]()
![]() By simplifying and solving this, we find that the ratio stabilizes as 1/. This factor is also valid for the ratio between the biggest circle and the middle circle:
By simplifying and solving this, we find that the ratio stabilizes as 1/. This factor is also valid for the ratio between the biggest circle and the middle circle:

Then, we can endlessly continue to shrink the circles and hence to narrow down the domain of the transcendental Thing to its 1/ factor.
![]() …∞
…∞
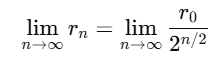
The limit of the radius, as we continue to shrink it by the factor 1/ , is 0.
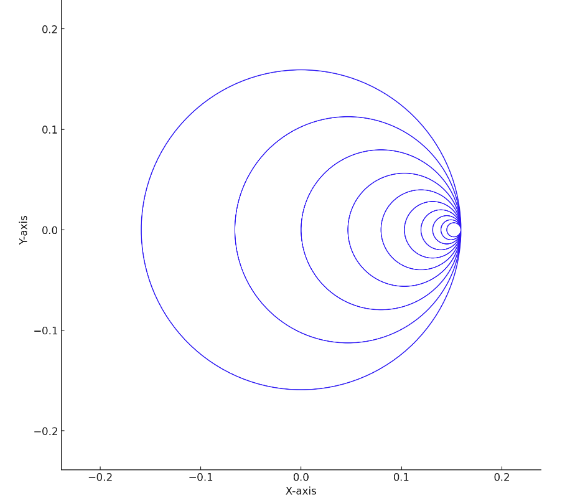
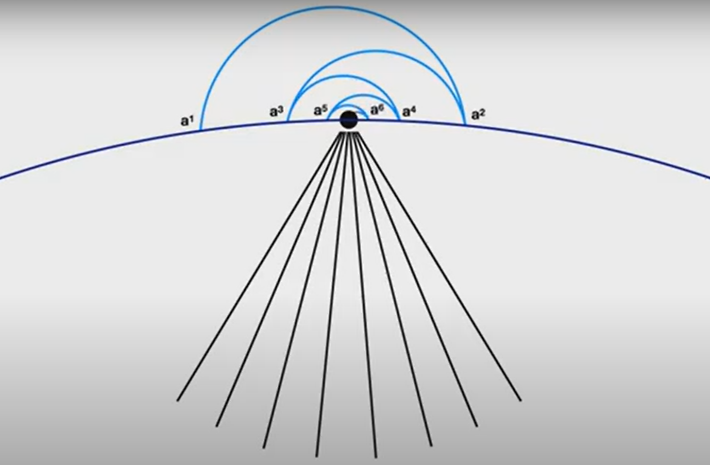
Here is the scaled visualization showing the sequence of shrinking circles. Each circle is tangent to the previous one and shrinks by a factor of 1/. The circles are drawn starting from a common tangent point, and the pattern repeats infinitely, illustrating the progressive decrease in size.
Implications of Orthogonality: The radius factor 1/ isn’t arbitrary. It relates to the scaling properties needed to maintain orthogonality through inversions. We are back to here:
The calculation of ρ=1/ not only solidifies the geometric structure underlying our discussion but also represents the recursive shrinking process inherent in the exploration of both mathematical and psychoanalytic truths. The psychological truth is metaphorized here with the transcendental number of . There is something transcendental, unreachable, unexplainable akin to the lacanian Real, in rotation as the fruit of orthogonality. Each step in this process, whether it be reducing the radius of a circle or peeling back layers of the Real as the Thing, brings us closer to an essential, yet elusive, core: the Point.
Conclusion: The Hidden Dimensions of Inversion Circles
The calculated ratio of 1/ between the radii of each circle and its inversion circle is not merely a mathematical curiosity. This ratio, which governs the recursive shrinking of circles, reflects the underlying geometry of desire itself symbolized with the transcendental Thing that shifts itself unchanged into the next circle—a geometry where each step towards the elusive objet petit a, leads to a further fractal unfolding of the psyche.
But what truly lies beneath this ratio is the implication that within every structure of desire, there exists a hidden locus where the symbolic and the real continually intersect and diverge in their orthogonal proportionality: there is no space of rotation, space is the rotation. The inversion circle is more than just a geometric construct; it is a metaphor for the perpetual tension between what can be symbolized and what remains beyond symbolization, between the algebraic (rooted in structure) and the transcendental (eluding structure). Each circle, as the inversion of its predecessor and successor, encapsulates a dynamic process where these two structures interact. As we go deeper into this process, the closer we get to an essential core, a point of convergence where the algebraic (≃Symbolic) gives way to the transcendental (≃Real.) Yet, this point is paradoxically unreachable, perpetually receding as we approach it—echoing Lacan’s notion of desire as something always deferred, never fully grasped.
This insight also challenges us to consider what remains unseen in the fractal paths that like this one have the same factor of 1/ (figure below). In the context of fractals and their scaling properties, the factor 1/ appears notably in the study of geometric transformations like rotations and dilations in higher dimensions.

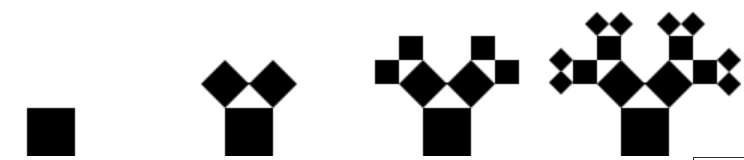
The Pythagorean fractal tree beautifully demonstrates how pure orthogonality can generate a rotational space. Rooted in the Pythagorean theorem, each iteration of the fractal maintains orthogonal angles, yet introduces a subtle rotation with a scaling factor of 1/. This scaling factor reveals the fractal’s intrinsic rotational nature, transforming a purely orthogonal structure into a dynamic, self-similar space. Thus, from the rigid orthogonality of right-angled triangles emerge captivating rotational patterns.
1.Original German words: Frisch weht der Wind/Der Heimat zu/Mein Irisch Kind/Wo weilest du? ↑
2.Kunze, Don.. The Logic of Phantasy: Lacan’s Slide-Rule Analogy. YouTube, 16 June 2022, The Logic of Phantasy: Lacan’s Slide-Rule Analogy (youtube.com)]. Accessed 24.08.2024. ↑